2014年度秋期の情報処理技術者試験（応用情報技術者試験の午前、高度試験の午前Ⅰ）で、カルノー図が出ました。2009年度の試験制度改定以来、応用情報と高度試験の午前でカルノー図が出るのは初めてです。

　応用情報や高度試験を受験する方なら、論理演算の知識はあると思います。変数A～Dに0を入れたり1を入れたりして、頑張れば正解にたどり着きます。ただ、考え込むと5分くらいは時間を使ってしまうでしょう。最初の問1がこれだから、焦った人も多そうです。

 

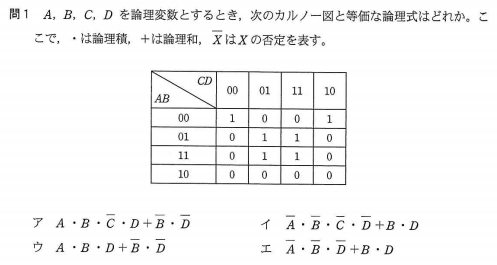
　カルノー図を知っていると、この問題は一瞬で解けます。



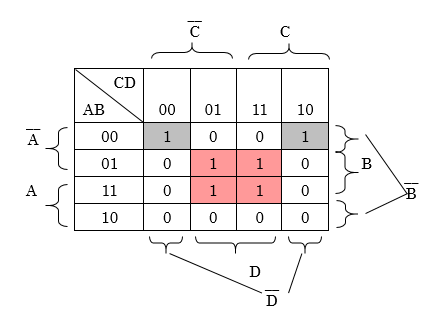
　グレーの部分の「1」は、AとBとDが重なる領域なので、論理積A・B・Dで表されます。
　赤の部分の「1」は、BとDが重なる領域なので、論理積B・Dで表されます。
　したがって、カルノー図全体としては、「A・B・D + B・D」になります。

　カルノー図を知らなくても頑張れば解けますが、知っていれば一瞬で解けるという、いい問題でした。